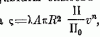Балистика внешняя
Балистика внешняя исследует движение снаряда по вылете из орудия.
С давнего времени математики занимались изучением движения артиллерийских снарядов.
Галилей доказал, что кривая, описываемая снарядом, была бы параболой, если бы не было сопротивления воздуха. Ньютон на основании своих опытов пришел к заключению, что сопротивление воздуха пропорционально квадрату скорости. Эйлер, Лежандр и др. также принимали его пропорциональным квадрату скорости.
Аналитические выражения сопротивления воздуха выводились и теоретически, и на основании опытных данных. Ньютон первый попытался сделать это, исходя из рассмотрения удара тела, которому сообщена поступательная скорость, о воздух, предполагаемый находящимся в покое. Были делаемы попытки найти выражения сопротивления воздуха, основываясь на формулах истечения жидкости (Дюпре, Себер и Валье, на механической теории газов и др. соображениях.
Опыты Маха (1887 г.) и Бойса (1892 г.) фотографирования летящего снаряда с воздушными волнами, его сопровождающими, показывают, что часть энергии снаряда расходуется на образование этих волн в воздухе. За невозможностью принять в расчет всех обстоятельств движения снаряда в воздухе, приходится выражение для сопротивления воздуха выводить в предположении, что равнодействующая сопротивления прямо противоположна направлению движения, — что справедливо только для сферических не вращающихся снарядов и для продолговатых, когда их ось совпадает с направлением движения. При сказанном допущении получают выражения для составляющих сопротивление воздуха по оси снаряда и по перпендикулярному к ней направлению и для момента пары сопротивления. Робинс первый произвел (в 1742 г.) систематические опыты над сопротивлением сферическим пулям; затем Гютон в Вуличе (1787-91 гг.) — над сферическими снарядами.
В 1839 и 1840 гг. были произведены опыты в Меце Пиобером, Мореном и Дидионом. При этих опытах для определения скоростей употреблялся балистический маятник.
При применении электричества к измерению скорости снарядов в двух точках траектории эти опыты были повторены, и произведены такие же опыты для продолговатых снарядов Башфортом в Англии (1865-80 гг.), генералом Маиевским в Спб. (1868—69 гг.), на заводе Круппа (1881—1890 г.г.) и Хожелем в Голландии (1884 г.). Результаты опытов выражают одночленом вида
, где ? — коэффициент, зависящий от формы головной части снаряда и обстоятельств, сопровождающих стрельбу, А — численный коэффициент, ? — отношение окружности к её диаметру, R — радиус цилиндрической части снаряда, ? — плотность воздуха при стрельбе и ?0 = 1,206 кг — плотность воздуха при 15° Ц, давлении атмосферы 750 мм. и влажности 50%.
Коэффициент A и показатель n, определенные из опыта, различны для разных скоростей.
В настоящее время почти повсюду пользуются формулами генерал Маиевского для скоростей не больше 550 м, а для скоростей бо?льших (до 1.000 м) — формулами генерала Н. Забудского; по этим формулам сопротивление воздуха при малых скоростях пропорционально квадрату скорости; при близких к скорости звука (340 м) сопротивление возрастет значительно быстрее квадратов скоростей (п доходит до 5), а при скоростях, превосходящих 550 м, — медленнее, чем квадраты скоростей.
При изучении движения снарядов рассматривают сначала их движение в безвоздушном пространстве под действием только силы тяжести, затем переходят к выводу дифференциальных уравнений движения не вращающегося сферического снаряда под действием силы тяжести и сопротивления воздуха; в этом случае движение происходит в вертикальной плоскости стрельбы; наконец, переходят к выводу дифференциальных уравнений движения снарядов, получающих вращение.
Т. к. силу тяжести можно принять направленной по вертикали, то траектория снаряда в пустоте получает вид параболы. Рассматривая дифференциальные уравнения движения не вращающегося снаряда в вертикальной плоскости стрельбы, С. Робер указал следующие главные свойства траектории: она выгнута выше горизонта; вершина её находится ближе к точке падения; угол падения больше угла бросания; горизонтальная проекция скорости постепенно убывает; наименьшая скорость и наибольшая кривизна находятся за вершиной; траектория имеет ассимптоту в нисходящей ветви и др.
Генералом Забудским еще добавлено, что время полета в нисходящей ветви более, чем в восходящей, и исследовано изменение вертикальной проекции скорости.
При движении снаряда в пустоте угол наибольшей дальности 45°; при движении же снаряда в воздухе (при постоянной плотности последнего на всем пути) этот угол вообще меньше 45°, но могут быть случаи, указанные Астие, Сиаччи и Забудским, когда этот угол больше 45°.
Иван Бернули (1719 г.), Даламбер (1744 г.) и другие дают способы решения дифференциальных уравнений движения не вращающегося снаряда при сопротивлении, пропорционально n-ой степени скорости. При этом простейшее выражение определяет точно только зависимость горизонтальной скорости от угла наклонения траектории; выражение же ординат траектории и времени полета в зависимости от угла наклонения приводятся к квадратурам, для пользования которыми нужны таблицы.
Для интегрирования дифференциальных уравнений движения предлагались различные приближенные способы. Наиболее удобный и общепринятый способ основан на введении Дидионом постоянной, причем при решении задач навесной стрельбы траекторию необходимо вычислять по частям.
В 1880 г. Сиаччи предложил весьма удобный для практики способ решения задач прицельной стрельбы, повсеместно употребляемый. Он принимает для сопротивления воздуха выражения, пропорциональные n-ой степени скорости, разные для различных пределов скоростей, и интегрирует дифференциальные уравнения движения приближенно, введя некоторую постоянную.
Для удобного решения задач составлены таблицы, приводимые в различных сочинениях. Способ Сиаччи оказывается неточным для задач навесной стрельбы. Для решения задач навесной стрельбы, когда начальная скорость не более 240 м, следует принимать сопротивление пропорциональным квадрату скорости с постоянным коэффициентом и применять таблицы Отто и графа Гревеница, измененные Сиаччи и Лордильоном.
Для точного же вычисления траектории, когда начальная скорость превосходит 240 м, следует ее разбивать на части и принимать для каждой из них различные выражения сопротивления воздуха, пропорциональные некоторой степени скорости, причем координаты траектории и времена придется вычислять при помощи квадратур.
В виду утомительности последнего, прибегают к способу и таблицам Башфорта, принимающего сопротивление пропорциональным кубу скорости, но с переменным коэффициентом, зависящим от скорости, или к способу, основанному на применении таблиц, составленных Сиаччи для прицельной стрельбы, причем траекторию разбивают на части и принимают для каждой части различные коэффициенты (при употреблении таблиц Башфорта) или произвольные постоянные (при пользовании таблицами Сиаччи).
Для решения практических вопросов Баллистики прибегают к упрощенным приемам.
Для решения задач навесной стрельбы для начальных скоростей в пределах от 240 до 650 м можно применять способ Забудского, основанный на допущении, что сопротивление пропорционально 4-й степени скорости, причем коэффициент сопротивления определяется для каждой задачи в зависимости от начальной и наименьшей скоростей. При весьма больших скоростях, превосходящих 650 м, приходится траекторию разбивать на три части, причем первую и последнюю части вычислять по способу Сиаччи, а среднюю — по способу Забудского.
Влияние вращательного движения сферических снарядов на траекторию было исследовано Пуассоном в случае, когда центр тяжести совпадает с центром фигуры, и в случае малого эксцентриситета. Остроградский предпринял (но не окончил) изыскания по тому же предмету при любой величине эксцентриситета сферических снарядов.
Опыты Магнуса (1852 г.) показали, что при движении в воздухе вращающихся снарядов происходит увеличение давления на одной части поверхности и уменьшение давления на другой, смотря по тому, происходит ли вращение этих частей в противоположную или в одну и ту же сторону с поступательным их движением. Разность этих давлений составляет причину отклонения эксцентрических сферических и дискообразных снарядов.
Первые существенные теоретические исследования над вращающимися около оси продолговатыми снарядами принадлежат итальянскому артиллеристу гр. С. Роберу (1859 г.), мемуары которого послужили исходною точкою для исследования генерал Маиевского.
Исследование этого вопроса начинается с изучения конического движения оси снаряда относительно понижающейся касательной к траектории, под действием пары сопротивления воздуха. На приборе Магнуса можно изучить коническое движение по модели продолговатого снаряда. Аналитические исследования привели Маиевского к заключению, что ось фигуры снаряда, когда поступательная скорость не слишком мала, имеет колебательное движение вокруг понижающейся касательной, и позволили изучить свойства этого движения для случая прицельной стрельбы.
Французскому артиллеристу де-Спарр удалось привести задачу к квадратурам в случае прицельной стрельбы, когда угол между осью фигуры и касательной мал. Этот вывод генералом Забудским обобщен для навесной стрельбы, и им указаны приближенные способы вычисления углов, определяющих положение оси снаряда по отношению к понижающейся касательной к траектории для всех случаев стрельбы. Кроме того, исследованием движения продолговатых снарядов занимались Вуич, Мюзо, Валье, Кранц, Гринхил и др.
Для правильного полета продолговатого снаряда, — как говорят, устойчивости его на полете, — необходимо определенное соотношение между угловою скоростью вращения снаряда около оси и его конструктивными данными; формула, связывающая упомянутые данные и выведенная генерал Забудским, дает результаты, согласные с опытом.
Вращательное движение продолговатого снаряда оказывает вообще слабое влияние на проекцию поступательного движения на плоскость стрельбы. При навесной стрельбе вращательное движение снаряда около его оси может оказать влияние на дальность. В 1908 г. выяснено, на основании результатов стрельбы, что с увеличением угловой скорости вращения снаряда замечается увеличение дальности.
Боковое отклонение продолговатого снаряда, выстрелянного из нарезных орудий, называют деривацией; опыт и исследование показывают, что при принятом у нас вращении снаряда слева-вверх-направо (правая нарезка), если смотреть по направлению стрельбы, и при расположении центра сопротивления впереди центра тяжести, деривация получается вправо; при расположении центра сопротивления позади центра тяжести — деривация получается влево; при левой нарезке — наоборот.
Маиевский вывел простую формулу для вычисления деривации в случае прицельной стрельбы, которую можно применять и в случае навесной стрельбы. Законы движения сферических снарядов в твердых средах и формулы для вычисления углублений выведены Мецской комиссией на основании результатов стрельбы; этими же формулами пользуются для вычисления углублений продолговатых снарядов, подыскав из опыта численные коэффициенты.
Для определения живой силы снаряда (или скорости для данного снаряда), необходимой для пробивания плит различной толщины и различных качеств, имеется множество формул. Первые обстоятельные опыты пробивания железных броней были произведены в Англии, и на основании этих опытов Нобль вывел формулы. В настоящее время употребляется формула, выведенная на основании опытов в Гавре французским артиллеристом Жакоб-де-Маром для определения скорости снаряда данного калибра и веса, необходимой для пробивания стальной плиты определенной толщины и известных качеств (мягкой стали, гарвеированной или круппированной).
Для смягчения действия удара на снаряд при стрельбе по плитам с цементированной поверхностью адмиралом Макаровым было предложено снабжать снаряды стальным мягким колпачком (наконечником).
Опыты показывают, что проникание в цементированные плиты таких снарядов увеличивается по сравнению со снарядами без наконечника и в тем большей мере, чем скорость при ударе в плиту больше.
Для определения действия разрывных снарядов принимают, что при их разрыве в грунте объем образованной воронки пропорционален весу разрывного заряда и численным коэффициентам, зависящим от скорости падения снаряда и его формы, качества грунта и свойства взрывчатого вещества заряда.
Испанским артиллеристом де-ла-Лав даны формулы для вычисления воронки, когда получается несколько близких между собою попаданий в бруствер, и для вычисления воронки в каменных, кирпичных и бетонных одеждах.
Способы решения баллистических задач применяются для составления таблиц стрельбы.
Прежде все данные, помещенные в таблицах, определялись эмпирически; затем перешли к определению по способу наименьших квадратов зависимости между дистанциями и углами бросания, применяя формулу академика Чебышева, для чего производилось достаточное число выстрелов при одинаковых обстоятельствах на различные дистанции; остальные данные, входящие в таблицы, вычислялись приемами, указанными в баллистике. Вычисление табличных данных производится не на все дистанции, а на некоторые данные на остальных дистанциях получают по формулам или по кривым.
При составлении таблиц стрельбы по аэростатам необходимо графически изобразить траекторию снаряда, для чего придется разбивать её на части, и можно ее вычислять, применяя таблицы, составленные для прицельной стрельбы.
Если у Вас есть изображение или дополняющая информация к статье, пришлите пожалуйста.
Можно с помощью комментариев, персональных сообщений администратору или автору статьи!